티스토리 뷰
ㅇ베이즈 확률은 사장의 통계, 확률이라고 한다.
조건에 따라 사후확률이 바뀌므로 의사결정에 유용하게 활용된다.
ㅇ 베이즈 통계학은 면적으로 확률을 설명한다.
- 어떤 특정암에 걸릴 확률이 0.1%(0.001)이고,
암에 걸렸는지를 검사하는 간이검사법이 있는데
암에 걸린 사람은 95%(0.95)의 확률로 양성진단을 받고
건강한 사람도 2%(0.02)의 확률로 양성으로 오진한다.
그렇다면 이 검사에서 양성이라고 진단받았을 때
이암에 걸렸을 확률은 얼마일까?

ㅇ 사전확률 → 조건(관측, 정보) → 사후확률 : 조건에 따라 확률이 변한다.
*조건에서 관측된 정보가 없으면 0.5이다.
(위 문제에서 양성 오진 확률 0.05가 없다면 0.5이다.)
ㅇ 베타분포 : 베이지안분포에서 사전분포로 많이 쓰임
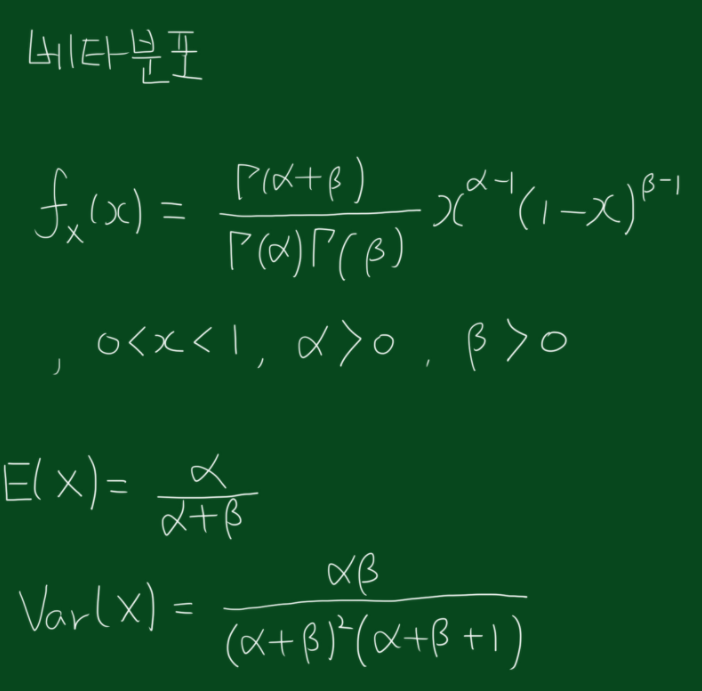
* 알파, 베타는 자연수임.
* 감마로 된 전체부분은 정수이고 적분값의 합이 1이 충족되는 조정수치임.
ㅇ 정규분포

- 정규분포에서 n개 관측 시 평균은 μ, 표준편차는 σ / (√n)
- 표준정규분포는 평균은 0이다.
ㅇ 정규분포 P(θ│x) 의 평균기대치(1회 관측) *P(θ│x) 는 조건확률
- x평균 기대치 = (1/σ1² × μ1 + 1/σ2² × μ2) / (1/σ1² + 1/σ2² )
* 사전분포(정규) : 평균 μ1, 표준편차 σ1
* 정보 x(정규분표 따름) : 평균 μ2, 표준편차 σ2
ㅇ 정규분포 P(θ│x) 의 평균기대치(n회 관측)
- x평균 기대치 = (1/σ1² × μ1 + n/σ2² × μ2) / (1/σ1² + n/σ2² )
* 사전분포(정규) : 평균 μ1, 표준편차 σ1
* 정보 x(정규분표 따름) : 평균 μ2, 표준편차 σ2
- x평균 기대치가 베타분포의 모양을 가짐
'투자를 현명하게 - 재테크 책을 읽고' 카테고리의 다른 글
| 17일만에 끝내는 해외주식 투자 / 장의성, 최우혁 / 메이크북스 (0) | 2021.03.25 |
|---|---|
| 워런 버핏은 무엇을 사고 사지 않는가 / 이항영, 장우석, 안석훈 / 예문 (0) | 2021.03.25 |
| 지금도 사야 할 아파트는 있다 / 김학렬(빠숑) / RH코리아 (0) | 2021.03.21 |
| 위기를 기회로 만드는 직장인 재테크 / 이호룡 / 북랩 (0) | 2021.03.21 |
| 머니쇼 2018 / 매일경제 서울머니쇼 취재팀 / (0) | 2021.03.16 |
- Total
- Today
- Yesterday
